Android Opengl Es 2.0 Draw Circle

In previous blogs, we drew triangles, squares, circles and cubes. Today we will depict cones, cylinders and spheres. After these basic conventional geometric shapes can be drawn, the drawing of other common geometric shapes is basically no problem for us.

Drawing cones
From the previous blog, we should all know that the focus of object drawing in OpenGL ES2.0 is to decompose the surface of the object into triangles. Later decomposition, the drawing volition not be a trouble. It is easy to remember of a cone as a circle and a cone. The vertex of the cone is identical to the vertex of the circle except that the coordinates of the central point of the cone have a "height". The circle has been drawn in Android OpenGLES 2.0 (4) - foursquare and circle, and then the cone is actually a small case for u.s.:

ArrayList<Bladder> pos=new ArrayList<>(); pos.add(0.0f); pos.add(0.0f); pos.add(elevation);        //Increase the meridian of the center of the circle relative to the edge to form a cone bladder angDegSpan=360f/due north; for(float i=0;i<360+angDegSpan;i+=angDegSpan){     pos.add((bladder) (radius*Math.sin(i*Math.PI/180f)));     pos.add((bladder)(radius*Math.cos(i*Math.PI/180f)));     pos.add(0.0f); } float[] d=new float[pos.size()];    //All vertices for (int i=0;i<d.length;i++){     d[i]=pos.get(i); }

We draw a cone by drawing a circle, then draw a circumvolve at the bottom of the cone, then that we go a cone:

We tin can see from the figure that we are not drawing the same color. If we use the same color, it is difficult to see the stereoscopic upshot of the cone. How does this color work? Let's look at its vertex shader (the chip shader is the same as before):

uniform mat4 vMatrix; varying vec4 vColor; attribute vec4 vPosition;  void main(){     gl_Position=vMatrix*vPosition;     if(vPosition.z!=0.0){         vColor=vec4(0.0,0.0,0.0,1.0);     }else{         vColor=vec4(0.nine,0.9,0.nine,ane.0);     } }

In the vertex shader, there is no incoming color, only the assignment is straight judged in the programme. Of course, there are likewise vertex color and edge color that tin can be imported from exterior. In the shader, we no longer simply assign values, only add together process control. In the next weblog, we volition focus on the Shader Linguistic communication GLSL, Android OpenGLES ii.0 (7) - the Shader Linguistic communication GLSL.

Drawing a cylinder
The cylinder is similar to the cone. We can split up the cylinder into ii upper and lower surfaces and add a cylinder. We haven't fatigued a cylinder before. How does it separate into triangles? We can understand the cylinder like the thought of dismantling the circle. Think of Zheng Mitsubishi Column, Zheng Ba Ling Cavalcade, Zheng Bai Ling Cavalcade... The more diamonds there are, the smoother it will be and the closer it will exist to the cylinder. And then each diamond (rectangle) volition exist broken into ii triangles. The vertex of the disassembly is:

ArrayList<Bladder> pos=new ArrayList<>(); float angDegSpan=360f/n; for(float i=0;i<360+angDegSpan;i+=angDegSpan){     pos.add together((bladder) (radius*Math.sin(i*Math.PI/180f)));     pos.add together((float)(radius*Math.cos(i*Math.PI/180f)));     pos.add(height);     pos.add together((bladder) (radius*Math.sin(i*Math.PI/180f)));     pos.add((bladder)(radius*Math.cos(i*Math.PI/180f)));     pos.add(0.0f); } float[] d=new float[pos.size()]; for (int i=0;i<d.length;i++){     d[i]=pos.get(i); }

So we can draw a cylinder, just depict a circle at the top and a circle at the bottom, and nosotros get a cylinder:

Drawing a sphere
Relative to conical cylinders, the disassembly of spheres is much more complicated. The mutual disassembly methods are to detach the spheres according to breadth and longitude and to detach the spheres co-ordinate to regular polyhedron.

Method of dismantling regular polyhedron:

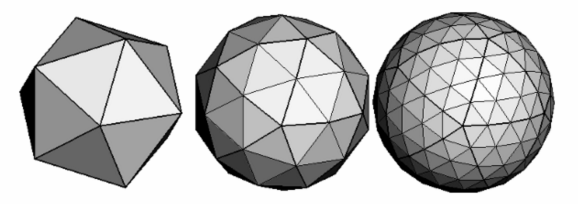
The method of longitude and latitude is dismantled (each block is regarded as a rectangle and and so dismantled into a triangle). :

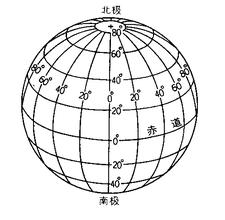
From the graph, we can also see that although polyhedron looks practiced, information technology is all the same easy to disassemble and calculate in the way of longitude and latitude, later on all, the law is so obvious.

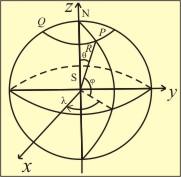
Coordinates of points on a sphere
The coordinates of the points on the sphere need to be known whether they are separate by breadth and longitude or by polyhedron. This is basic geometric cognition. If the center of the sphere is the coordinate heart and the radius of the sphere is R, so the coordinates of the points on the sphere are:
(R∗cos(ψ)∗sin(λ),R∗sin(ψ),R∗cos(ψ)∗cos(λ))
(R∗cos(ψ)∗sin(λ),R∗sin(ψ),R∗cos(ψ)∗cos(λ))

Among them, _is the bending between the line segment from the heart to the point and the xz plane, and lambda is the angle betwixt the projection of the line segment from the heart to the point on the xz airplane and the z axis. Graphical representation is every bit follows:

Disassembly vertex
The vertex assortment of the sphere is obtained past disassembling the sphere according to longitude and latitude.

ArrayList<Float> data=new ArrayList<>(); bladder r1,r2; float h1,h2; bladder sin,cos; for(bladder i=-ninety;i<90+stride;i+=pace){     r1 = (float)Math.cos(i * Math.PI / 180.0);     r2 = (float)Math.cos((i + step) * Math.PI / 180.0);     h1 = (float)Math.sin(i * Math.PI / 180.0);     h2 = (bladder)Math.sin((i + footstep) * Math.PI / 180.0);     // Fixed latitude, 360 caste rotation traverses a latitude line     float step2=footstep*2;     for (float j = 0.0f; j <360.0f+step; j +=step2 ) {         cos = (float) Math.cos(j * Math.PI / 180.0);         sin = -(float) Math.sin(j * Math.PI / 180.0);          data.add(r2 * cos);         data.add(h2);         data.add(r2 * sin);         data.add(r1 * cos);         data.add together(h1);         data.add(r1 * sin);     } } bladder[] f=new float[data.size()]; for(int i=0;i<f.length;i++){     f[i]=data.get(i); }

Once the vertices are obtained, the residuum of the piece of work is the same as the previous drawing of other graphics.

Alter the shader
If we go on to apply the conical shader, we will go such a brawl:

Information technology doesn't look much similar a ball. If it weren't for a white line, information technology wouldn't be a ball. Nosotros need to change the lower vertex shader to give information technology a iii-dimensional feel. Modify the vertex shader to:

uniform mat4 vMatrix; varying vec4 vColor; attribute vec4 vPosition;  void main(){     gl_Position=vMatrix*vPosition;     float color;     if(vPosition.z>0.0){         color=vPosition.z;     }else{         color=-vPosition.z;     }     vColor=vec4(color,color,colour,1.0); }

Run it, nosotros get the following results, so that we tin can say it's a ball.

smithweandstaid1983.blogspot.com

Source: https://programmer.group/android-opengles-2.0-building-cones-cylinders-and-spheres.html

Share this post